Current triangles
If you have read the section on "Dead reckoning", you will know that it is crucial always to know your position when sailing – and if you cannot be absolutely sure (for example due to fog) then it is important to estimate as precisely as at all possible!
In the exercise "Dead reckoning" you were to sail from Zealand to Jutland and you were only told how much time had elapsed and which course and speed you had held. But what if there had been a current? How do you find out how much the current influences the ship’s course and speed?
If you have the opportunity to watch the current run past a point, a buoy or something else stationary, it is possible with a little practice to estimate its strength in exactly the same way as the ship’s own speed can be determined. In its simplest form it is possible to steer a little into the current but this does not solve the problem of the influence on the ship's speed. For this a so-called current triangle is used.
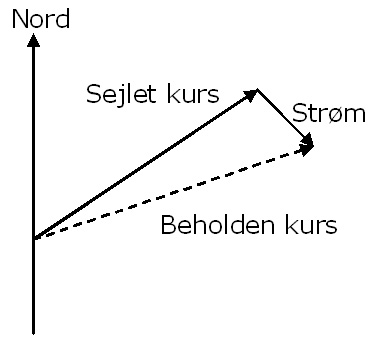
The ship's course and speed can be drawn as a line of a particular length and direction – a vector. The scale is irrelevant. Try for example drawing a speed vector on course 110°, 5 knots, where 1 knot is shown by making the arrow 5 cm long.
Vectors can be directly added on to one another. If your ship on course 110°, making 5 knots, is influenced by a southwards (180°) current of 1.5 knots, you draw this in extension of the first vector. The result, the so-called course made good is the vector, which extends from the beginning of the first vector to the end of the second. In reality you are moving on course 125° at 5.7 knots.
Set and drift
This exercise introduces vectors, graphic addition and subtraction of vectors, the parallelogram of forces.
It can also be used as an introduction to further work with calculus of vectors, for example to introduce co-ordinates.
Discuss whether current triangles may have been used in the Viking Age. Does this make sense when navigating without using a compass marked in degrees? Is it possible to do this mentally so the principle is used in a more intuitive way without allocating precise values? Think of other areas where one compensates without thinking for some force or other – ball games in windy weather…
This exercise can be solved on the exercise sheet Dead reckoning.
Subject: Maths.
Suitable for age: 16-20 years.
If, on the other hand, you want to find out how to steer to end up on a particular course, the situation becomes a little more complicated. You do not know the speed made good but only the sailed speed – the length of the vector you want to find. First, the direction and speed of the current is drawn in, and then the course made good is drawn from the same starting point and extending a good distance out (the speed made good is not yet known). From the end of the current vector the sailed speed is added with a pair of compasses so that it cuts the course made good. The sailed course and the speed made good can now be read off.
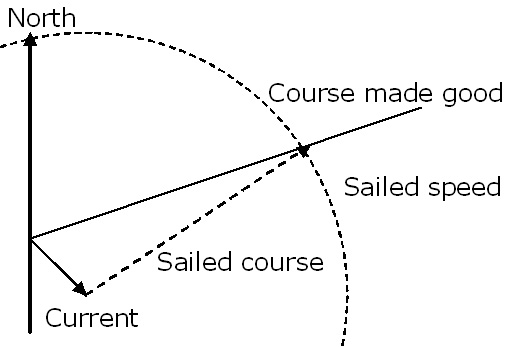
It is also possible to go the opposite way and calculate the current: If you know that you have, in reality, moved along a particular vector and if you have also kept a check on the course you steered to achieve this, the vectors can be subtracted from one another: The two vectors are drawn from the same starting point. The vector, which can be drawn between the two end points, reveals the current.
Exercises:
- You are sailing on course 56° at 3.5 knots. The current is running southwest at 0.5 knots. What is your course made good?
- You measure your speed at 4.5 knots. You wish to proceed along a course made good of 275°, but there is a northwards current of 1 knot. In which direction must you steer (we will ignore the influence of the wind)? With what speed will you proceed towards your goal?
- You have steered 126° and measured your speed at 4.5 knots. When you see land, you can establish that in reality you have travelled along course 130° at 6 knots. What was the current?
- Find more examples yourself...
- Mental arithmetic: You are sailing 300° in a northward current. Is the current with or against you?
- You change course to 260°. Is the current with or against you now?
- Return to the exercise sheet Dead reckoning. Imagine that from 13:02 to 15:17 you have sailed in a 3 knot southwards current. How does this influence your dead reckoning and what will happen if you overlook the current? What course should you steer in order to stay on the course made good of 211°?
Read more
Tools
- Dead reckoning EN.pdf
- exercise sheet